* 이 글은 홍콩과기대 김성훈 교수님의 무료 동영상 강좌 "모두를 위한 머신러닝과 딥러닝 강의"를 보고 요점을 정리한 글 입니다.
Q-Network
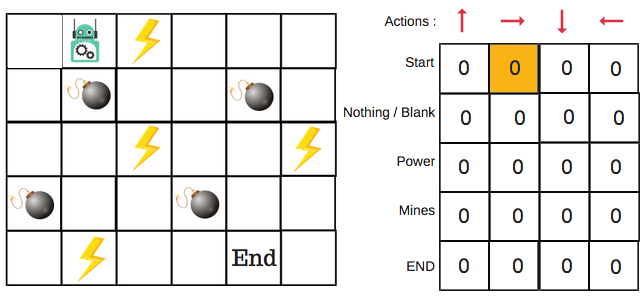
Q-Table을 사용한 학습은 굉장히 쉽게 사용할 수 있습니다. 하지만 카메라를 통해 입력받은 화면에 대한 Q-Table은 엄청난 크기를 가지게 됩니다. Reinforcement Learning(강화 학습)을 사용할 수 있는 대부분이 이런 카메라를 통해 입력받는 화면을 사용해야 하기 때문에 Q-Table를 대신할 새로운 방법을 생각해야 했습니다.
이런 Q-Table을 대신하여 문제를 해결하기 위해서 선택된 방법이 바로 Neural Network(신경망)입니다. 이 Neural network를 사용한 Reinforcement Learning을 다른 말로 Q-Network 라고 부릅니다. Reinforcement Learning 에서의 Neural Network는 현재 State를 입력하면 취할수 있는 모든 Action들에 대한 Q값들을 반환하는 형태입니다.
Q-Learning에서 학습방법의 기본적인 부분은 Linear Regression(t선형 회귀)의 방법과 유사합니다. 현재 State의 정보 s를 입력값으로 Neural Network에 넣고 나오는 결과값을 Linear Regression의 결과값과 유사한 Ws라고 설정하고 또한 Q-Learning에서의 Cost Function도 Linear Regression과 유사하게 Ws와 Label값인 y의 차를 제곱한 값들을 모두 더한것으로 설정합니다. 이것을 수식으로 표현하면 Equation (1)과 같습니다.
| $$ cost(W) = \frac{1}{m} \sum_{i=1}^{m} (Ws - y)^2 $$ | (1) |
위의 수식에서 사용한 Label 값인 y는 Q-Learning 알고리즘에서 배웠던 Equation (2)의 값을 갖습니다.
| $$ r + \gamma \max_{a'} Q(s', a') $$ | (2) |
또한 Neural Network에서 설정된 Weight값에 따라서 값이 위에서 가정한 Ws값이 달라지기 때문에 Weight를 theta라고 본다면 위의 Ws를 좀 더 정확하게 Equation (3)으로 표현할 수 있습니다.
| $$ \hat{Q}(s, a|\theta) $$ | (3) |
Linear Regression에서 사용하는 방법과 유사하게 학습하면서 Cost Function의 결과값을 최소화 해야하기 때문에 이 모든 것을 고려해서 Q-Network의 학습을 수식으로 표현하면 Equation (4)와 같이 표현할 수 있습니다.
| $$ \min_\theta \sum_{t=0}^T [\hat{Q}(s_t, a_t|\theta) - (r_t + \gamma \max_{a'} \hat{Q}(s_{t+1}, a'|\theta))]^2 $$ | (4) |
물론 마지막 Goal State에 도달했는냐 아니냐에 따라서 라벨 값은 다를 수 있습니다. 기본적인 공식은 위와 같지만 마지막 State의 여부까지 고려한다면 식은 Equation (5), (6)과 같이 쓸 수 있을 것입니다.
| $$ y_j = \begin{cases} r_j & \text{for terminal } s_{t+1} \\ r_j + \gamma \max_{a'} Q(s_{t+1}, a'|\theta) & \text{for non-terminal } s_{t+1} \end{cases} $$ |
(5) |
| $$ \min_\theta \sum_{i} (\hat{Q}(s_i, a_i|\theta) - y_j)^2 $$ | (6) |
Q-Network의 대표적인 예로는 DQN이 있습니다.
'강의 Study > 모두를 위한 머신러닝과 딥러닝 강의-시즌 RL' 카테고리의 다른 글
| [시즌RL].Lecture 7 - DQN (0) | 2024.07.15 |
|---|---|
| [시즌RL].Lecture 5 - Q-Learning in non-deterministic world (0) | 2024.07.13 |
| [시즌RL].Lecture 4 - Q-Learning exploit&exploration and discounted reward (2) | 2024.07.12 |
| [시즌RL].Lecture 3 - Dummy Q-Learning (0) | 2024.07.11 |
| [시즌RL].Lecture 2 - OpenAI GYM 게임해보기 (0) | 2024.07.10 |

